电场下阴极射线偏转电场内阴极射线偏转

【电场下阴极射线偏转电场内阴极射线偏转】正如我们在上节课上所说，汤姆逊研究阴极射线的基本方法是将电场和磁场应用于阴极射线。通过研究阴极射线在电场力和磁场力作用下的偏转，最终计算阴极射线的速度和荷质比。
这涉及到两个重要的基本知识，电场和电场力、磁场和磁场力。今天，让我们先谈谈人类对电力的研究历史，以及电场是什么？

文章插图
其实上节课结束的时候，我可以直接告诉你汤姆逊的测量结果，发现电子就结束了。
然而，我认为作为一系列科普，普及一些基础知识是非常必要的。否则，很多事情都是一句话带来的，最后我们还是听不懂。
就像在大多数科普书籍中，关于电子发现是一句话，说汤姆逊给阴极射线增加了电场和磁场，最后测量了荷质比，发现了电子，并获得了诺贝尔奖。看完之后，我看起来很困惑，不知道细节，感觉很痛苦。
好了，我们就不多说闲话了，开始今天的话题。

文章插图
在第一篇文章中，我们说了人类对电现象的发现和研究历史，知道了电有同性相斥和异性相吸的性质，那么接下来我们就需要对电之间的排斥力和吸引力做定量的研究，也就是用数学方法把它们之间的力描述出来。
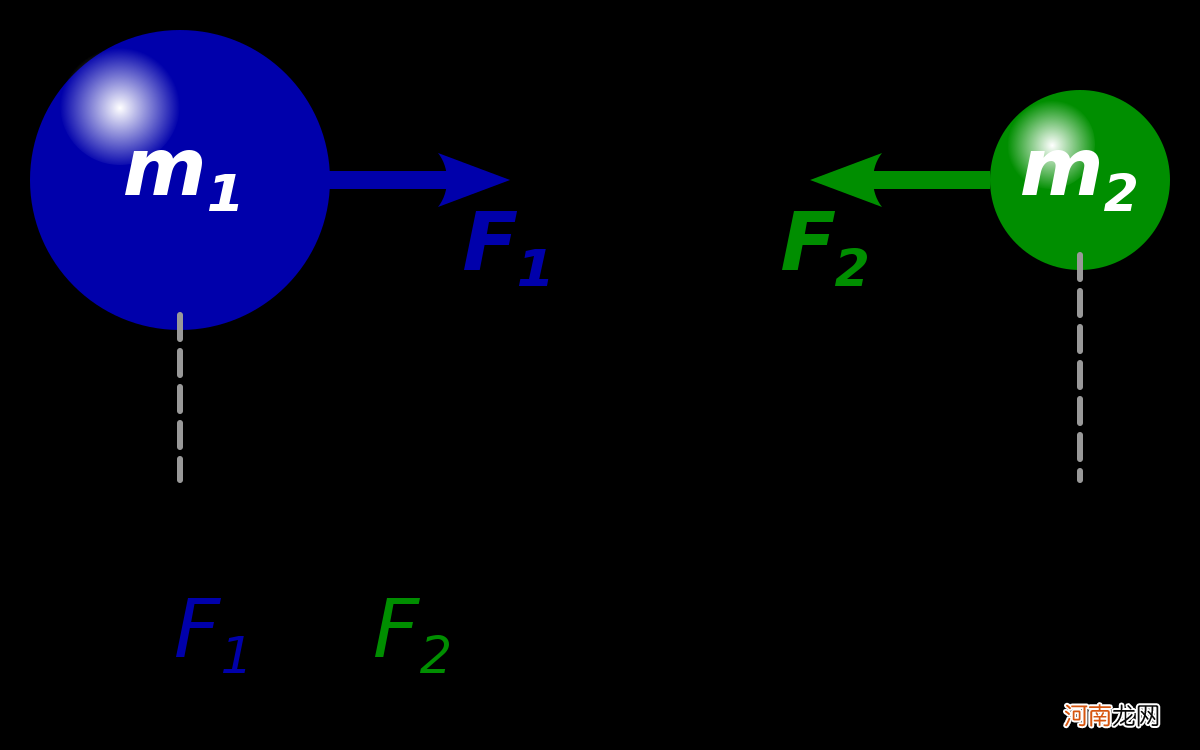
事实上，关于电力的研究没什么好说的，因为电力的方程完全是根据葫芦画的。这个葫芦是牛顿的万有引力公式。
重力与两个物体的质量相比，与它们之间的距离相比，这种关系非常符合人们的直觉，质量大，重力大，距离远，重力小，所以人们猜测电力可能是一样的。
它也与距离平方成反比，与粒子携带的电荷成正比。可见，电力方程和引力方程体现了物理对称之美。

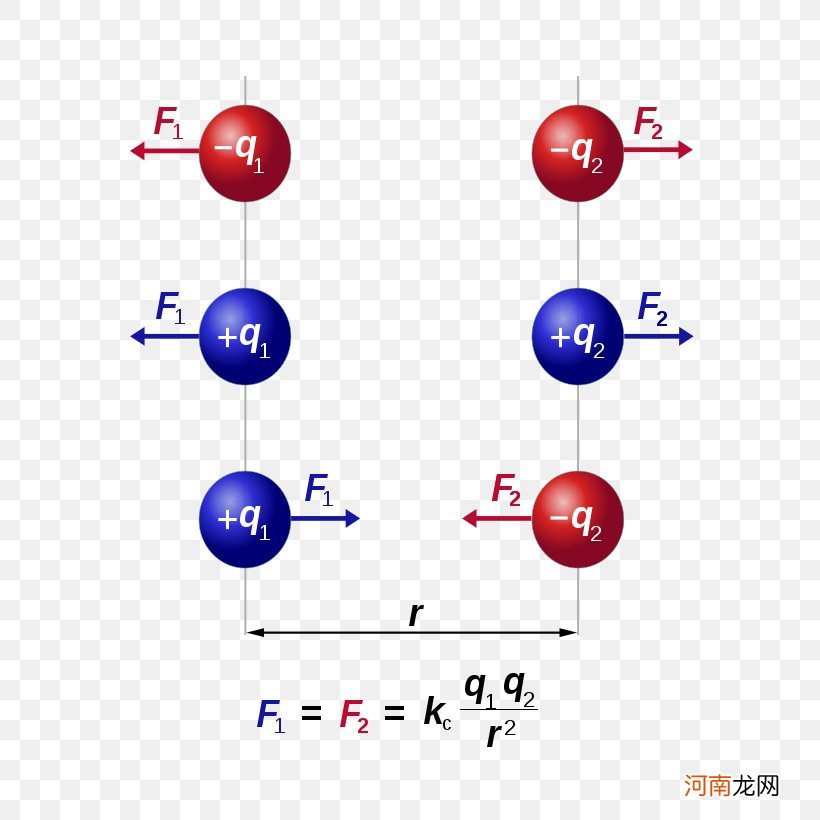
文章插图
如此重要的公式是完全猜测的。事实上，只要符合实验结果，猜测也是一种科学的方法。普朗克的黑体辐射公式也聚集在一起，薛定谔的波动方程也有很大的猜测。

文章插图
1785年，法国1785年制作了第一次最令人信服的电力方程实验，其实验装置与亨利相比·可文迪许测量引力常数的扭秤很像，也就是我们现在在图中看到的样子，通过这个装置，库仑确定了电力方程的准确性。

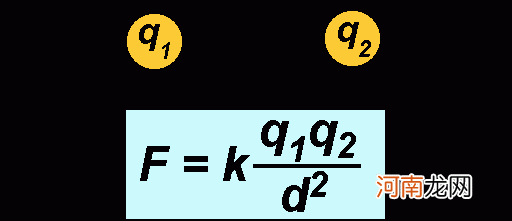
文章插图
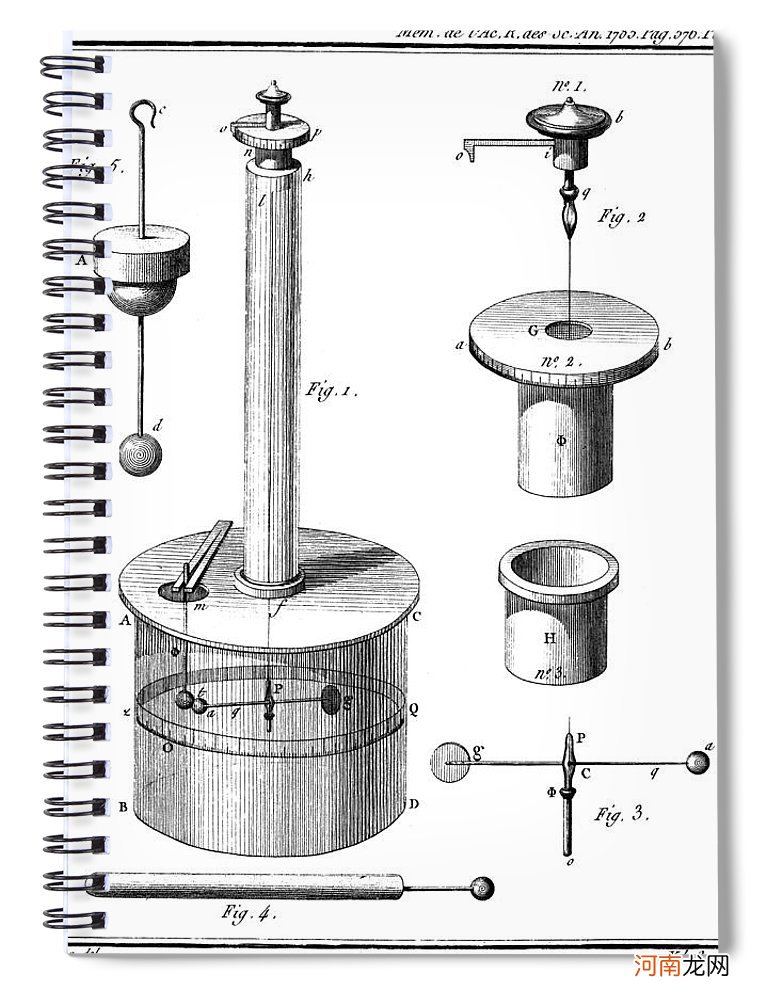
因此，电力方程是粒子1作用于粒子2的电力=Ke×粒子1的电荷×电荷/粒子1与粒子2的距离^2

文章插图
其中Ke它是静电常数，其值取决于力、电荷和距离所使用的单位，只能通过实验测量，在万有重力中G一样。
若电荷单位采用库仑，力单位采用牛顿，距单位采用米，则静电常数值为8.99×10^9牛·米2/库2

文章插图
现在让我们来看看静电方程，也被称为库仑定律。我们可以看到，颗粒产生的静电总是与它自己携带的电荷成正比。所以我们可以直接把方程中的K（Q?/r2）作为一个整体，这个整体是一个比例系数，麦克斯韦称之为电场强度。
可以看出，电场的强度取决于产生电场的物体所携带的电荷以及受影响物体与其之间的距离，但与受影响物质的电荷和性质无关。

文章插图
所以引入电场强度只是为了方便计算，我们可以写库仑定律作用于带电体的电力=物体的电荷×电场强度。
根据上述公式，我们还可以看到，电场强度的单位是牛顿/库仑，这意味着单位电荷的力。因为力是矢量，电场强度也有方向。
正如我们在前一篇文章中所说，带正电荷的粒子产生的电场方向是从自身到外，带负电荷物体产生的电场方向是从物体到自身。
因此，带正电的物体的电场力方向与电场强度方向相同，带负电的物体的电场力方向与电场强度方向相反。想不想也没关系。让我解释一下电场。
电场是一个非常抽象的概念，因为我们看不见它，就像我上面提到的电场力的方向和电场强度的方向一样，我相信很多人不能理解，不用担心，因为法拉第发明了电场的图表，这给了我们一种直观的感觉。

文章插图
上图就是孤立电荷周围的电场线，可以看出正电荷的电场线向外，负电荷的电场线向内，这是人为规定的，每啥特殊的原因，毕竟谁也没有看到过电场长啥样子。
有了电场线，电场更容易理解，我们可以认为单位面积的电场线数量代表了当地电场的强度，所以我们可以理解为什么电场力与距离平方成反比，因为电荷越远，单位面积的电场线越少。

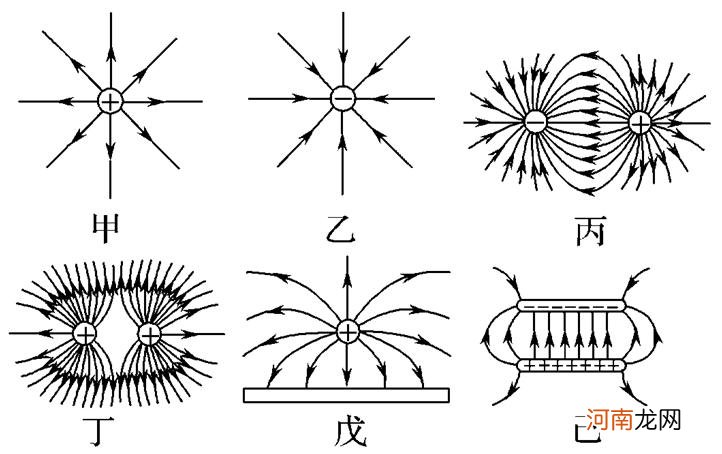
文章插图
上图是几种情况下的电场线。引入电场最大的意义在于我们对牛顿所说的力有不同的理解。在牛顿的框架下，力的概念非常模糊，甚至可以是超距效应。
有了场的概念，我们可以认为物体的力与扩散在空间中的地方相互作用。在现代物理学中，我们发现场是一个概念物体，或者是一种易于计算的数学技能，而是一个真正的物理物体，甚至比基本粒子更基本。
量子电动力学（QED）在中国，我们对电磁力有了更深的理解。带电物体之间产生力的原因是它们相互交换光子，光子受到电磁场的刺激。根据电磁力的相互作用，我们还根据葫芦画瓢，画出弱力和强力的作用模式，这也反映了自然的对称之美。后来，当我们谈论相互作用力时，我们也会谈论这些事情。
让我们谈谈在汤姆逊的实验中，阴极射线在电场力作用下的偏转。在他的实验中，汤姆逊使用的电场是由两个平行的带电金属板制成的，就像我们现在看到的。

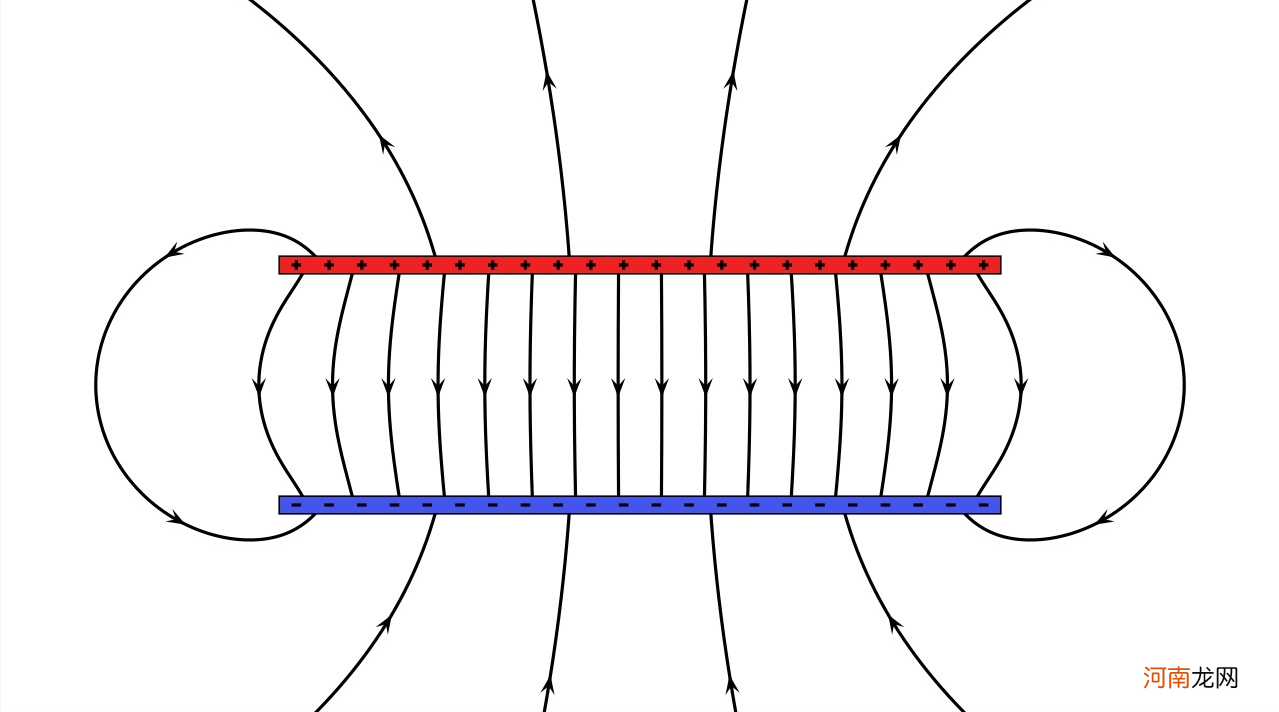
文章插图
金属板之间电场的方向垂直于金属板，且均匀，保证带电颗粒在其间飞行时的电力始终垂直于运动方向，力的大小在各处都是一样的。
而且有一点特别重要。两块金属板之间的电场强度与任何一块板之间的距离无关，因为正如我们刚才所说，电场强度等于单位面积内的电线数量。可以看出，在确定间距的带电金属板之间，电场线的数量是固定的。
因此，我们可以知道，在汤姆逊的实验中，电力等于电荷乘以电场强度，这里的电场强度是常数，所以我们可以根据上节课的公式知道：
电场力使阴极射线产生的位移=(粒子电荷×电场强度×偏转区长度×漂移区长度)/(粒子质量×粒子速度^2）.
接下来最重要的是计算金属板之间的电场强度，这实际上非常简单，两个金属板之间的电场强度等于电压除以金属板之间的距离。
为什么要这样计算？让我们先谈谈什么是电压。电压也称为电势。电势的定义是将带电颗粒的势能除以电荷。我们知道势能是一种能量形式，所以电压的单位是焦耳/库仑，这通常被称为伏特。
从电势单位焦耳/库仑可以看出，电势也可以用这种方式表示，一个库仑的电荷可以通过1伏特的电势差获得，即1焦耳。
因此，电池是一种提供电势差的装置。例如，电池的电压为2伏，对每个库仑电荷的工作为2焦耳。
当时汤姆逊给平行金属板施加的电压是225伏特，说明一库仑的电荷从一个金属板移动到另一个金属板。电池的工作是225焦耳，我们也知道工作等于力乘以距离，所以作用在每个库仑上的电场力。×金属板之间的距离=电池对每个库仑电荷的作用。
因此，每个库仑上的电场力=225焦/库÷0.015米(金属板之间的距离)=1.5×10^4牛/库。正如我们上面所说，每个库仑的力都是电场强度。
因此，电场强度等于电压除以金属板之间的距离。现在已经计算出电场强度，然后已知偏转区长度、漂移区长度和偏转距离。
因此，我们可以了解阴极射线粒子的电荷、质量和速度平方之间的关系。这是阴极射线的所有参数，阴极射线的所有参数。
正如上一篇文章所说，三个未知参数，一个方程当然不好，所以我们还需要给阴极射线施加磁场，然后得到另一组参数，最后得到阴极射线粒子的速度和荷载比，这是我们下一节课的内容。

电场下阴极射线偏转 电场内阴极射线偏转

电场下阴极射线偏转电场内阴极射线偏转