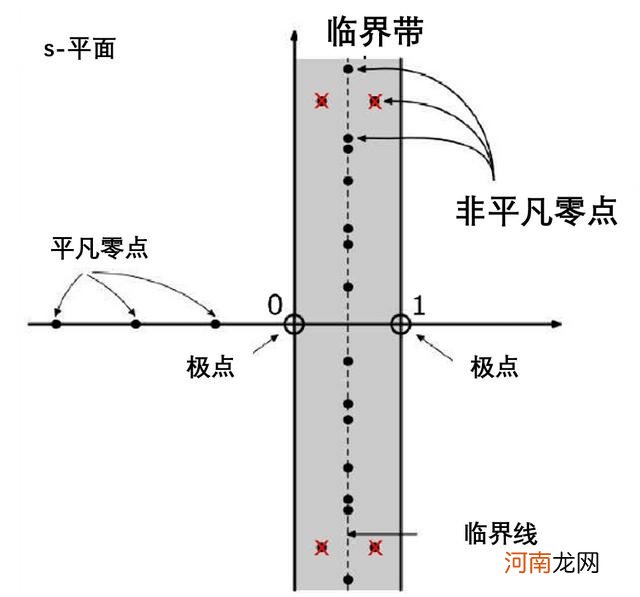
已知所有非平凡零都有0到1之间的实部 , 称为临界带 。结果是 , 如果s是一个非平凡零点(即ζ(s) = 0且s不是负偶数) , 那么对于一些值y , s = 1/2 + iy(即s的实部是1/2) , 这就是所谓的临界线 。
文章插图
伯奇和斯温纳顿-戴尔猜想
给定一条?上的椭圆曲线E , 其代数秩总是与解析秩重合吗?
椭圆曲线E , 为方程y^2=x^3+Ax+B的解集 , 且判别式?=-16(4A^3+ 27B^B)≠0 。这个约束条件保证了曲线足够好 。
文章插图
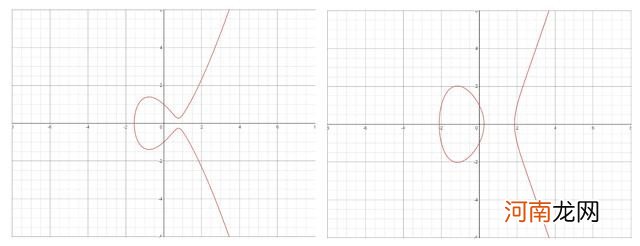
- 两个椭圆曲线 。左边:y^2=x^3-1.5x+1 。右边:y^2=x^3-4x+1
【6大地狱级的世界数学难题 世界上最诡异的数学题】
文章插图
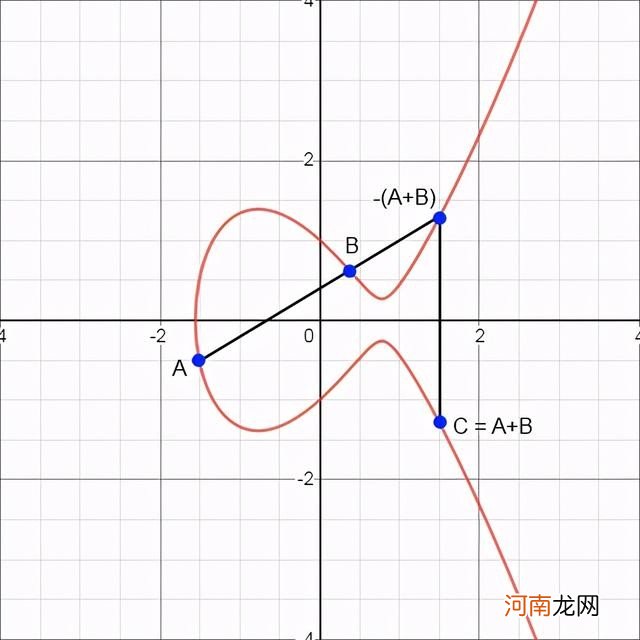
- 如何将两点A和B相加得到C
第一个自然的问题是 , 我们可以推断出E(?)的结构是什么?
莫德尔和威尔(Mordell and Weil)的结果告诉我们 , E(?)是有限生成的 , 可以写成:
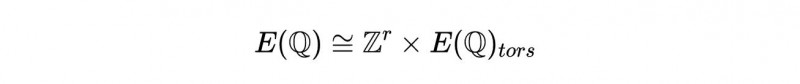
文章插图
其中E(?)_tors是E(?)中所有有有限顺序的点 。r被称为曲线E的代数秩 。
现在我们有了前半部分 。现在我们需要理解解析秩 。
现在让我们进一步限制解 , 考虑在有限域p上 , 其中p是一个素数 , 我们定义以下值:

文章插图
最后是E在s处的L级数:
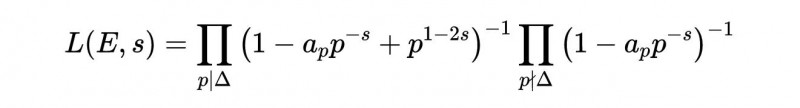
文章插图
回忆一下 , ?是椭圆曲线的判别式 。那么我们可以将L展开成一个泰勒级数 , 围绕s = 1展开:
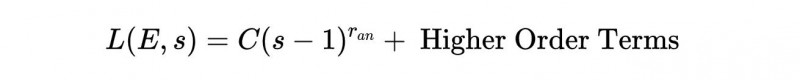
文章插图
这里 , r_an是曲线的解析秩 。
终于!我们可以把伯奇和斯温纳顿-戴尔猜想简单地写成:
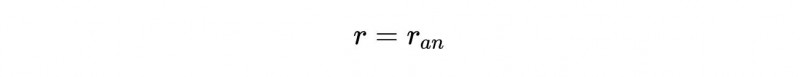
文章插图
这些都意味着什么呢?结果是 , 计算代数秩相当困难 , 而解析秩稍微容易一些 。这个猜想在解析领域和代数领域之间架起了一座桥梁 。
杨-米尔斯存在性与质量间隙
给定任何紧凑的简单规范群G , 在?? (?^4)上 , 是否存在一个非平凡量子杨-米尔斯理论 , 具有质量间隙 Δ > 0?
- 大班语言动物职业介绍所教案反思
- 大班语言活动给动物分房教案反思
- 大班美术活动会变的水果教案反思
- 大班语言活动心情预报教案反思
- 大班美术活动美丽的扇面教案反思
- 爱护鸟类和关爱大自然 大班美术活动树鸟的巧合教案反思
- 大班语言小兔逃跑教案反思
- 孩子最容易中招的3大传染高发疾病,家长该怎么做?
- 宝宝多大才能喝纯牛奶
- gb1354大米执行标准