6大地狱级的世界数学难题世界上最诡异的数学题

文章插图
在2000年之初，克雷数学研究所提出了七个问题，这些问题被认为是至今仍未解决的最困难的问题之一。解决其中任何一个问题都有100万美元的赏金。
在我写这篇文章的时候，只有庞加莱猜想得到了解决。格里戈里·佩雷尔曼（Grigori Perelman）在2003年给出了证明，并在2010年被正式授予千禧年奖，但他拒绝了。
我将首先介绍这个猜想（现在是定理），然后根据复杂度的增加顺序介绍剩下的未解决的问题。
庞加莱猜想
庞加莱猜想，拓扑学上的一颗明珠，揭开宇宙形状之谜
任何一个单连通的，闭的三维流形一定同胚于一个三维的球面。
让我们逐字分析一下。首先，流形是局部具有欧几里得空间性质的空间，在数学中用于描述几何形体。这意味着，如果你放大它，它看起来像一条线或一个平面或规则的三维空间等等。一个流形的例子是一个球体，如果你和它相差足够大并身处其中，它看起来是平的（就像你感觉地球是平的一样）。流形的维数就是它局部看起来像的空间的维数，例如，一个球局部看起来像一个平面（这意味着它有维数2），一个圆局部看起来像一条线（所以它有维数1），一个思维球体局部看起来像一个三维结构（这一定很神奇，但是我们无法想象）。
如果一个流形是紧凑且无边界的，那么这个流形就是封闭的（这是一个比较复杂且重要的拓补概念，需要另一篇文章来详细解释）。0和1之间的线段有0和1的边界，所以不是封闭的。圆没有边界，所以是封闭的。

文章插图

一种封闭的2维流形，叫做2维环面

如果一个流形没有“孔” ，则它是单连通的：

文章插图

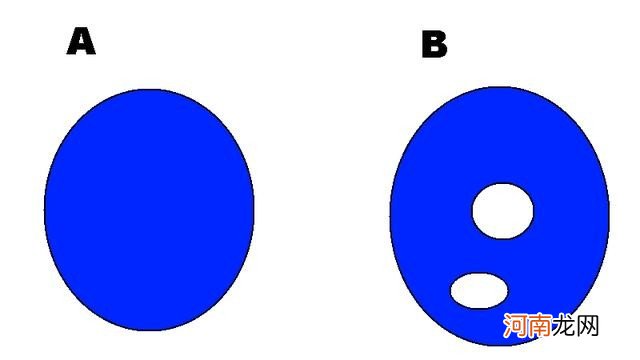
A是单连通空间， B不是单连通空间

等效的单连通表述是，每个环可以连续地收缩到一点。

文章插图

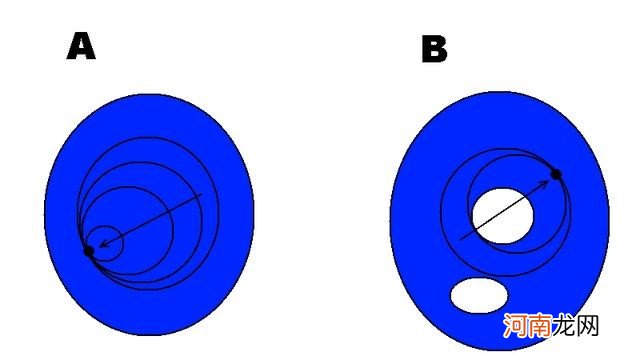
A中的一个环可以收紧到一个点；B中的一个环被一个孔“卡住” ，不能被收紧到一个点。

如果能连续地把一个变形成另一个，然后再变回来，那么这两个流形是同胚的（允许的变形包括拉伸、挤压和扭转，但不允许撕裂和穿孔）。这就引出了著名的甜甜圈和茶杯杯之间的比较（拓补上，它们是同一种东西）。

文章插图

把甜甜圈变形成茶杯

在拓扑学中，我们想对所有流形进行分类，其中在某个类中的所有流形都是彼此同胚的。在二维空间中，很容易看出，如果流形是封闭的且没有洞，那么它就相当于一个2维球体（圆面）。很容易确定一个2维流形是否同胚于2维球体。
庞加莱指出，这在三维中也是成立的，即任何封闭的，单连通的3维流形都同胚于3维球面。
2002年，格里戈里·佩雷尔曼通过使用“里奇流”证明了庞加莱猜想。
P vs NP
能否快速验证每个问题是否可以解决，并快速解决？

6大地狱级的世界数学难题 世界上最诡异的数学题

6大地狱级的世界数学难题世界上最诡异的数学题