地球到月球的直线距离是多少月球到地球的距离

简而言之，到月球的平均距离是384403公里（238857英里）。但是你在思考最终的答案之前，你需要考虑几件事。
首先，请注意“平均”这个词的使用。这指的是月球以椭圆轨道绕地球运转，这意味着在某些时候，它会离得很远，而在其他时刻，它会离得更近。

文章插图
因此，这个数字384403公里是天文学家称之为半长轴的平均距离。在它最近的点（称为近地点），月球距离地球只有363104公里（225622英里）。
并且在它最远的点（称为远地点），月球的距离是406696公里（252088英里）。

文章插图
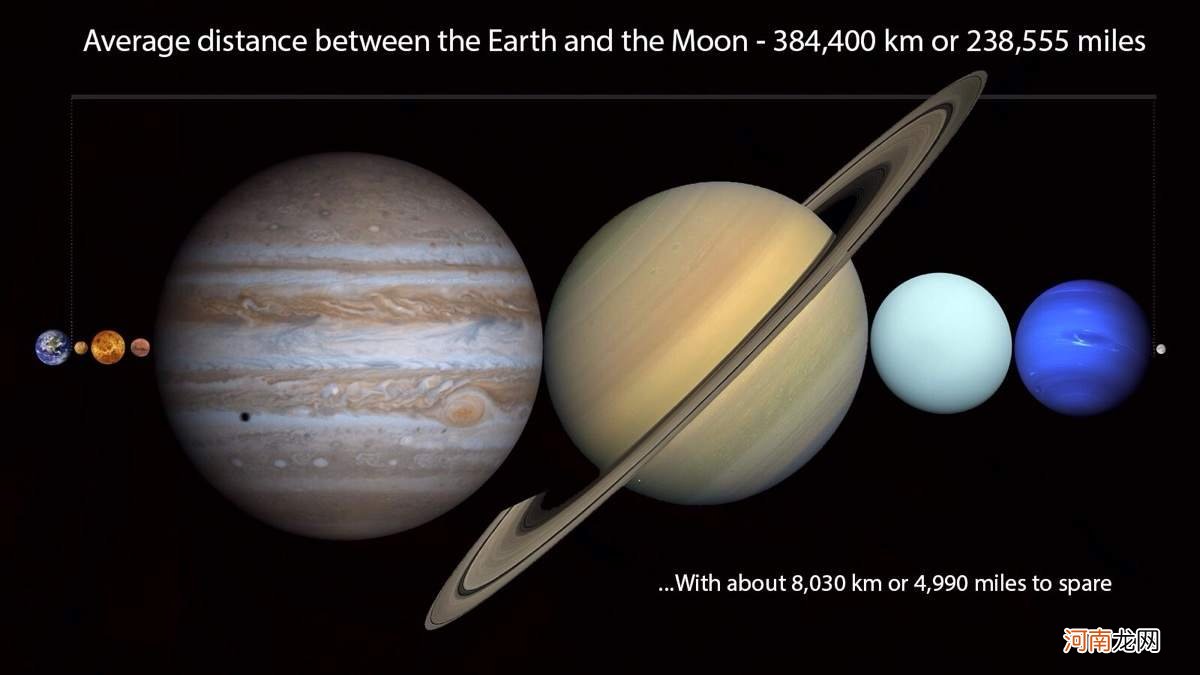
这意味着从地球到月球的距离可以变化43，592公里。这是一个相当大的差异，它可以使月球在轨道上的不同位置看起来大小截然不同。
例如，月球的大小可以从最近的时候到最远的时候变化超过15% 。

文章插图
它也可以对月球在其全相时的明亮程度产生巨大的影响。正如人们可能预期的那样，最亮的满月出现在月球离我们最近的时候，通常比最远的时候亮30% 。
当它是一个满月，它也就离我们最近，它被称为超级月亮；同样所知晓的学术名称—近地点-合月。

文章插图
要了解这一切是什么样子，请看戈达德太空飞行中心科学可视化工作室于2011年发布的动画。该动画每小时显示一年中月球的地心相位、振动、轴的位置角度和表观直径。

文章插图
在这一点上，一个很好的问题是：我们如何知道月球有多远？嗯，那要看我们什么时候开始了解地球了。
在古希腊时代，天文学家依靠简单的几何学、地球的直径(他们已经计算出相当于12875公里(或8000英里))和阴影的测量来做出第一次(相对)准确的估计。

文章插图
在观察和记录了阴影在漫长的历史过程中是如何工作的，古希腊人已经确定，当一个物体被放置在太阳前面时，它产生的阴影的长度总是物体本身直径的108倍。
因此，一个直径为2.5厘米（1英寸）的球，放在太阳和地面之间的棍子上，会产生一个延伸为270厘米（108英寸）的三角形阴影。
这一推理随后被用于月食和日食现象。

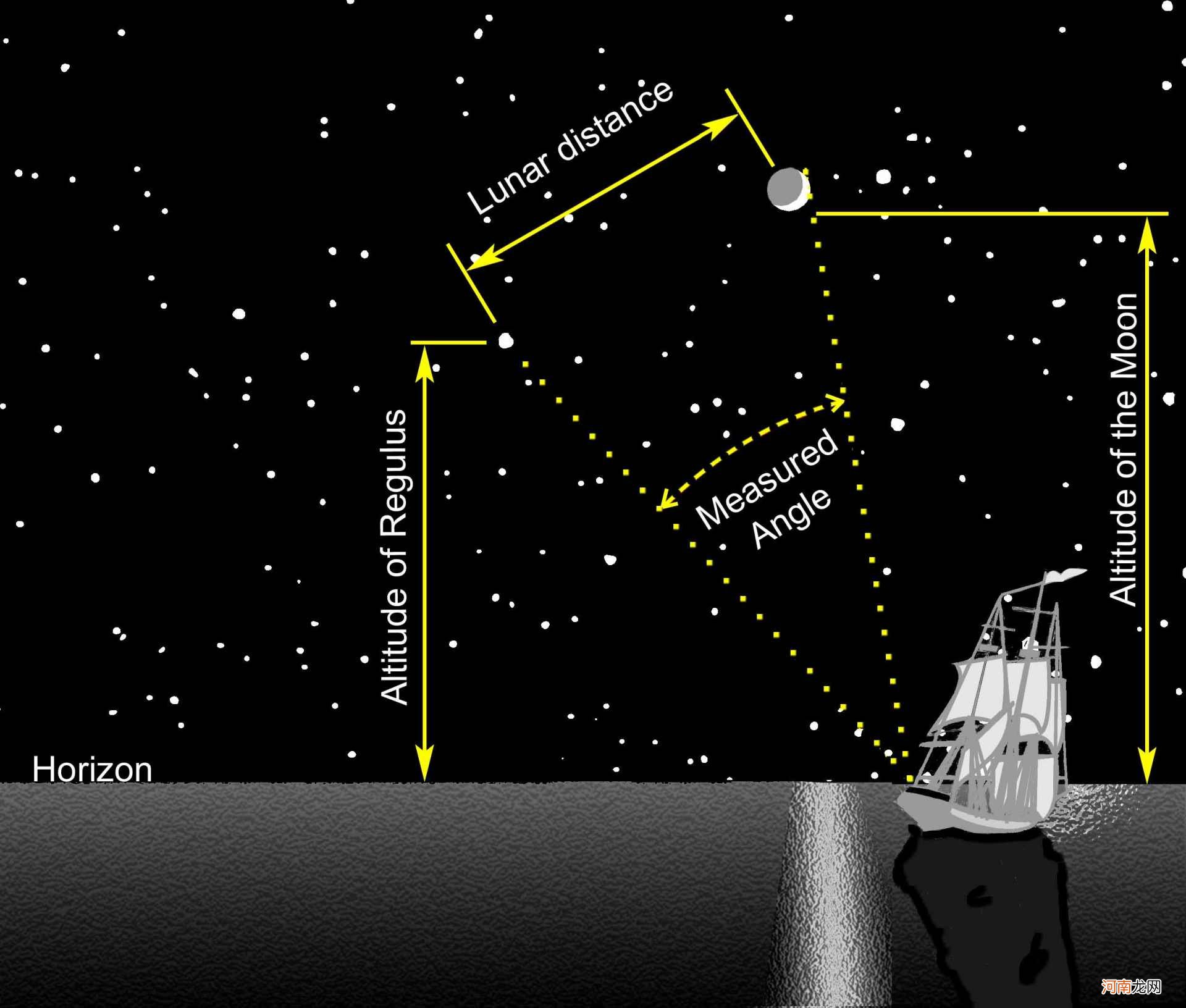
文章插图
在前者中，他们发现月球被地球的阴影挡住了，而且阴影的宽度大约是月球的2.5倍。在后者中，他们注意到月球的大小和距离足以挡住太阳。
更重要的是，它将产生的阴影终止于地球，并以与地球阴影相同的角度结束-使它们成为同一三角形的不同大小形式。
通过对地球直径的计算，希腊人推断，更大的三角形将可用来在12875公里/8000英里的基础上测量一个地球直径，这个三角形的长度为139万公里(86.4万英里) 。
另一个三角形将相当于2.5个月球直径宽。因为这两个三角形是成比例的，为2.5个月球轨道高。

文章插图
将这两个三角形加在一起将产生相当于3.5个月球轨道的当量，这将产生最大的三角形，并(再一次，相对)准确地测量地球和月球之间的距离。
换句话说，距离是139万公里(86.4万英里)除以3.5，等于大约39.75万公里(24.7万英里) 。虽然不是很棒，但对古人来说还不错！

地球到月球的直线距离是多少 月球到地球的距离

地球到月球的直线距离是多少月球到地球的距离