由①-② ， 得：

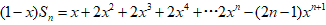
文章插图

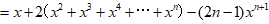
文章插图

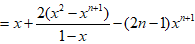
文章插图
于是

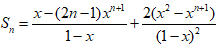
文章插图
四、用化差相减法适用于分式形式的通项公式 ， 基本原理是把一项拆成两个或多个的差的形式 ， 即

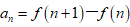
文章插图
 ， 然后累加时中间的许多项可以抵消 。裂项凑错位相加特征 ， 注意前后式子相等 ， 如果不相等就要乘以一个系数 。
常用公式：

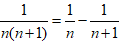
文章插图
 ， 

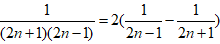
文章插图
 ， 

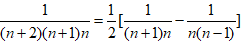
文章插图
 ， 

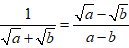
文章插图
（a≠0） ， 

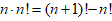
文章插图
例5、求数列

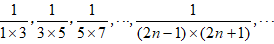
文章插图
的前n求和 。解：

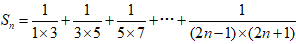
文章插图

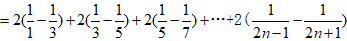
文章插图

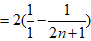
文章插图

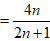
文章插图
例6、求数列

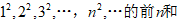
文章插图
。解：∵

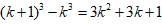
文章插图
∴

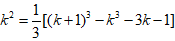
文章插图
基本原理点拨：代数式变形凑相消特征：

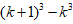
文章插图
 ， 由此可联想求更高次方幂的n项和 。如：

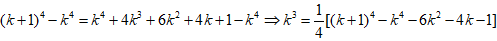
文章插图
至此 ， 一般规律就出现了 ， 通过变形整理便可求出

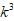
文章插图
的n项的和 ， 以此类推 ， 求n次方幂的问题就能彻底解决 。从而

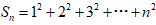
文章插图

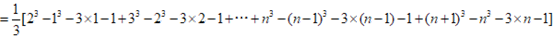
文章插图

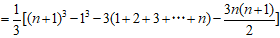
文章插图

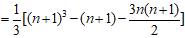
文章插图

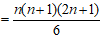
文章插图
五、利用组合数求和公式法利用这个组合数公式 ， 求某些特殊数列的前n和颇为方便 。因为

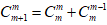
文章插图
 ， 则

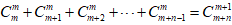
文章插图
。例7、求数列

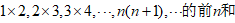
文章插图
解：∵

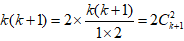
• 凯撒旅业：在积极探索目的地、新零售等创新业务
• 绝对值不等式的解法
• 东阿阿胶、伊利等“国家企业技术中心”资格被撤
• 尽显尊贵 吉利嘉际头等舱特别版车型首发
• 长城发布GWM品牌 哈弗H6等车型在老挝上市
• 广汽丰田赛那等 下周上市/预售新车前瞻
• 一 宝马iX/凌放等 广州车展热点车前瞻
• 蛋糕1磅怎么算的 1磅等于多少斤
• 一磅等于多少斤 1磅等于多少斤kg
• 捷途X90子龙凌云出击 鲲鹏加持性能再高一等