三垂线定理及其逆定理

新课标高中数学中，淡化了“三垂线定理及逆定理” ，但我们认为：三垂线定理还是非常好用的。至少用它来证明有关题目，会简捷得多!
(一)温故知新，引入课题大家已经学习了直线和平面的垂直关系，学新课之前，让我们作个简单的回顾：
1.直线和平面垂直的定义?
2.直线和平面垂直的判定定理?

文章插图

(二)猜想推测，激发兴趣

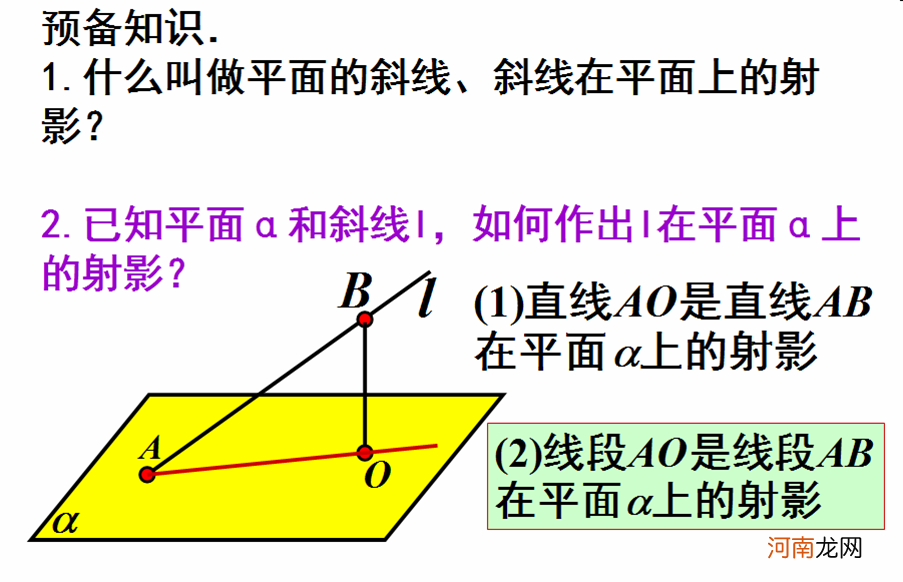
文章插图

文章插图

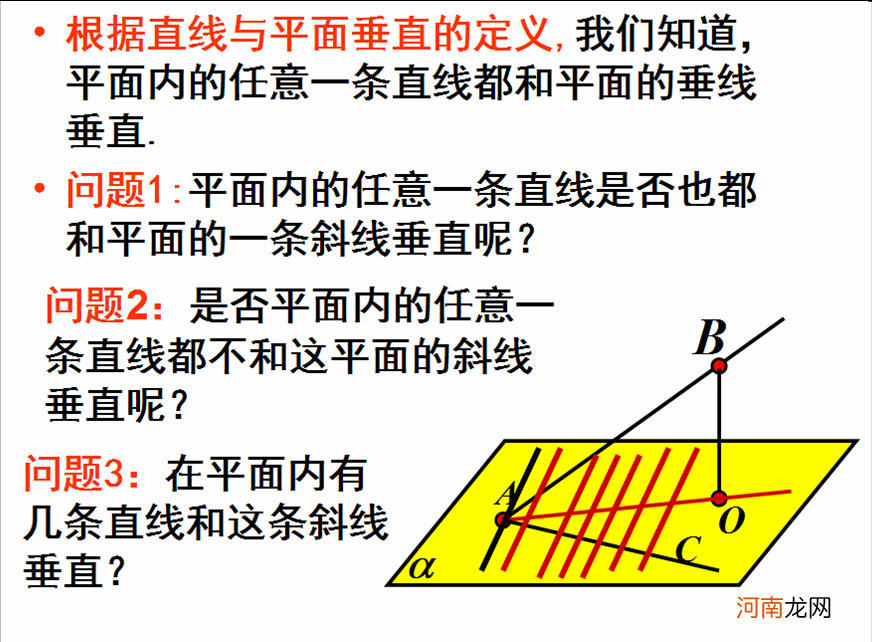
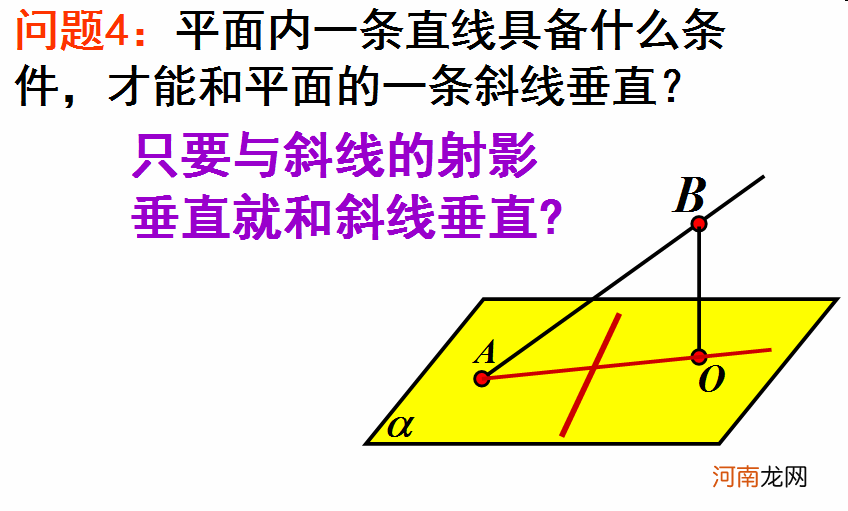
(三)层层推进，证明定理我们在讨论立体空间时，通常会想把空间的问题转化为平面问题，那有没有什么方法可以帮助我们将空间与平面联系在一起呢? ? 今天我们学习的内容，就可以把空间垂直的问题转化为平面垂直的问题。这就是:三垂线定理与三垂线逆定理 .
我们先来看一下三垂线定理及逆定理的描述。
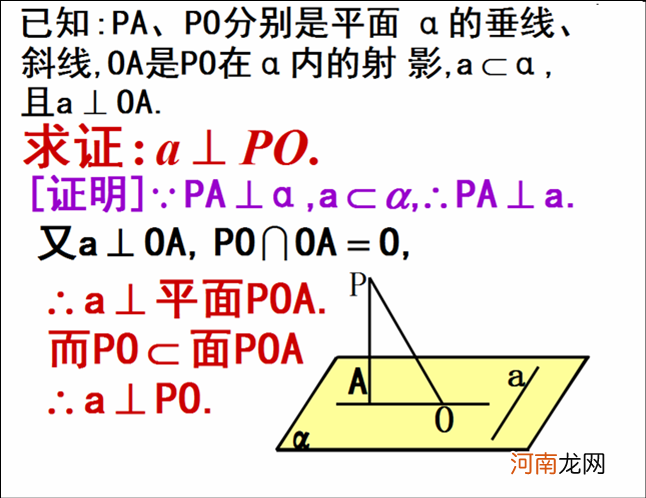
1、三垂线定理：平面内的一条直线，如果和这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。
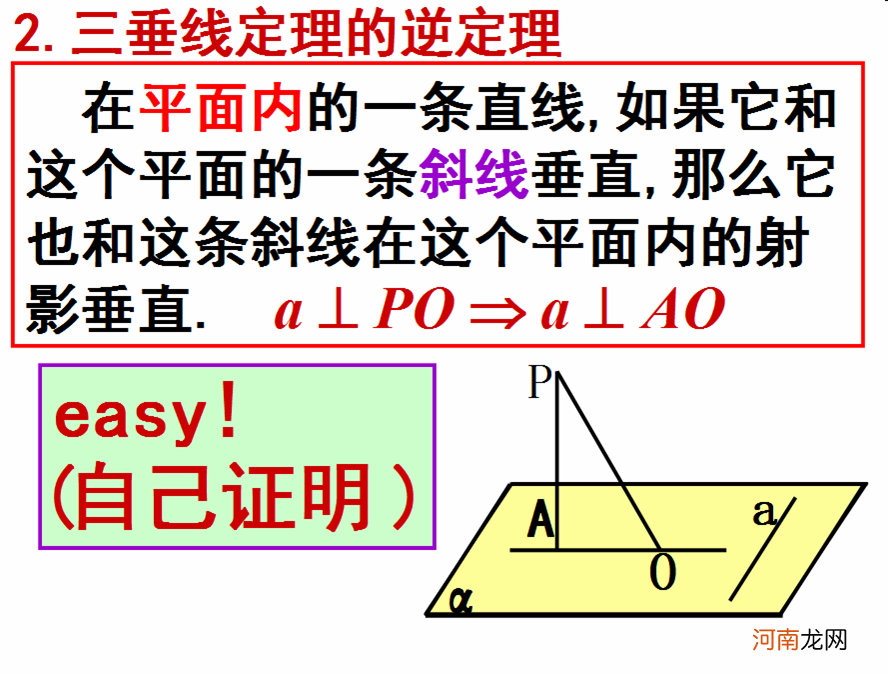
【三垂线定理及其逆定理】2、三垂线定理的逆定理：如果平面内一条直线和该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

文章插图

文章插图

具体在图中体现为：我们将OP称为平面的斜线， PA是平面的垂线， AO是OP在平面内的射影， a是平面内的一条直线，若a与AO垂直，则l也与PO垂直，反之亦然。
其实三垂线定理从证明的角度看可以认为是线面垂直转化关系的一个常用推论.这是一个标准的从线线垂直(一般是共面)转化为线面垂直又转化为新的线线垂直(一般是异面)的立体几何推理过程。
但换一个观点和角度来看，三垂线定理的价值在于将一个需要进行多次转化而且模式基本确定的证明过程以定理的形式规范下来，这使得在相关的证明(之后还有计算)过程中书写难度得到有效降低，在部分复杂题目中更是如此。而从很多立体几何题目设计的思路来看，经常会出现两条看似无关直线(一般是异面)的关系问题，一般方法是让他们在不同平面中分别找关系，然后利用一个桥梁进行沟通;三垂线定理正是提供了这样一个可以进行简便沟通的方式。
而更为重要的是，在三垂线定理中，最重要的其实并不是斜线或者射影(尽管它们分别是条件和结论) ，而是平面的垂线!有了这个垂线的存在，才会使得两条异面直线建立关系;有了这个垂线，才能形成相应的平面和直角三角形从而便于计算;而同样也是因为有了这条垂线，使得直线和平面所称的角，以及升级版的平面和平面所成的角(二面角)出现并有了用平面角度量其大小的方式。在这个意义上，三垂线定理的模型也包含了重要的计算角度的方式，即“异面角”平面化，把空间中的角转化为平面几何特别是直角三角形中相应角度和边长的计算。