sin30度是多少 sin30度是什么梗( 二 )

13.你知道吗?空间立体几何中，以下命题均错：
(1)空间中不同三点确定一个平面；
(2)垂直同一直线的两直线平行；
(3)两组对边分别相等的四边形是平行四边形；
(4)如果一条直线与平面内无数条直线垂直，则直线垂直平面；
(5)有两个面互相平行，其余各面都是平行四边形的几何体是棱柱；
(6)有一个面是多边形，其余各面都是三角形的几何体都是棱锥注：对初中生不适用。
14.一个小知识点：所有棱长均相等的棱锥可以是三、四、五棱锥。
15.求f(x)=∣x-1∣+∣x-2∣+∣x-3∣+…+∣x-n∣(n为正整数)的最小值。
答案为：当n为奇数，最小值为(n2-1)/4 ，在x=(n+1)/2时取到;当n为偶数时，最小值为n2/4 ，在x=n/2或n/2+1时取到。
16.√〔(a2+b2)〕/2≥(a+b)/2≥√ab≥2ab/(a+b)(a、b为正数，是统一定义域)
17.椭圆中焦点三角形面积公式：S=b2tan(A/2)
在双曲线中：S=b2/tan(A/2)
说明：适用于焦点在x轴，且标准的圆锥曲线。A为两焦半径夹角。
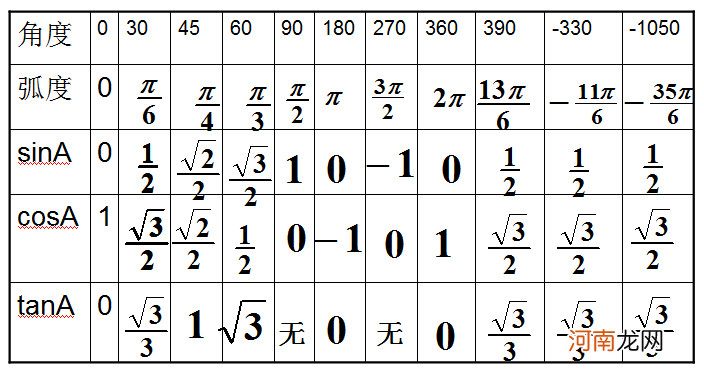
18.爆强定理：空间向量三公式解决所有题目：

文章插图
cosA=|{向量a.向量b｝/[向量a的模×向量b的模]|
A为线线夹角；A为线面夹角(但是公式中cos换成sin)；A为面面夹角注：以上角范围均为[0 ，派/2] 。

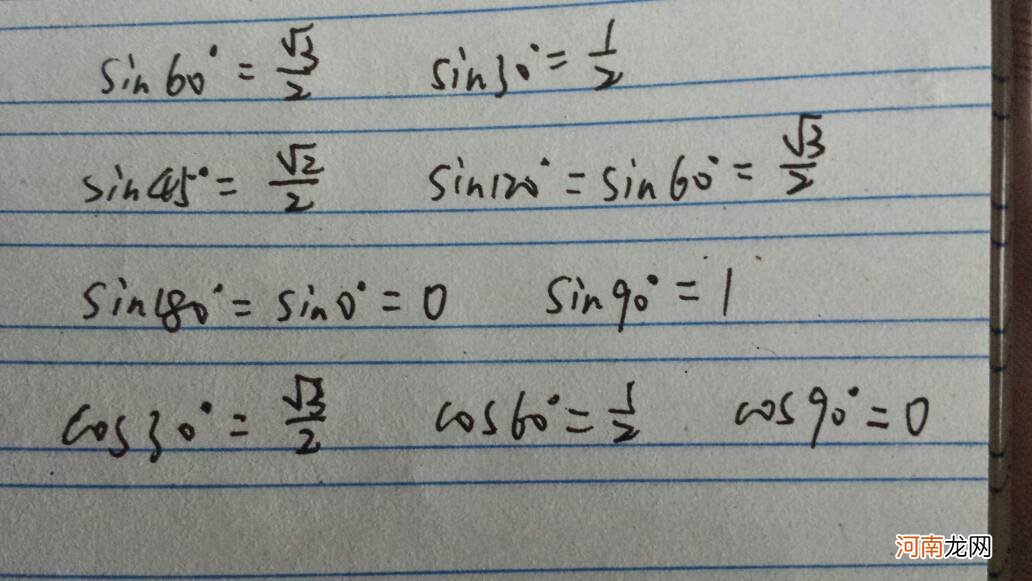
文章插图
19.爆强公式12+22+32+…+n2=1/6(n)(n+1)(2n+1)；
123+223+323+…+n23=1/4(n2)(n+1)2
20.爆强切线方程记忆方法：写成对称形式，换一个x ，换一个y 。
举例说明：对于y2=2px可以写成y×y=px+px再把(xo ， yo)带入其中一个得：y×yo=pxo+px
21.爆强定理：(a+b+c)2n的展开式[合并之后]的项数为：Cn+22 ， n+2在下， 2在上
22.[转化思想]切线长l=√(d2-r2)d表示圆外一点到圆心得距离， r为圆半径，而d最小为圆心到直线的距离。
23.对于y2=2px ，过焦点的互相垂直的两弦AB、CD ，它们的和最小为8p 。
爆强定理的证明：对于y2=2px ，设过焦点的弦倾斜角为A.那么弦长可表示为2p/〔(sinA)2〕，所以与之垂直的弦长为2p/[(cosA)2] ，所以求和再据三角知识可知。(题目的意思就是弦AB过焦点， CD过焦点，且AB垂直于CD)
24.关于一个重要绝对值不等式的介绍爆强：∣|a|-|b|∣≤∣a±b∣≤∣a∣+∣b∣
25.关于解决证明含ln的不等式的一种思路：
举例说明：证明1+1/2+1/3+…+1/n>ln(n+1)把左边看成是1/n求和，右边看成是Sn 。
解：令an=1/n ，令Sn=ln(n+1) ，则bn=ln(n+1)-lnn ，那么只需证an>bn即可，根据定积分知识画出y=1/x的图。an=1×1/n=矩形面积>曲线下面积=bn 。当然前面要证明1>ln2 。
注：仅供有能力的童鞋参考!!另外对于这种方法可以推广，就是把左边、右边看成是数列求和，证面积大小即可。说明：前提是含ln 。
26.爆强简洁公式：向量a在向量b上的射影是：〔向量a×向量b的数量积〕/[向量b的模] 。记忆方法：在哪投影除以哪个的模
27.说明一个易错点：若f(x+a)[a任意]为奇函数，那么得到的结论是f(x+a)=-f(-x+a)〔等式右边不是-f(-x-a)〕，同理如果f(x+a)为偶函数，可得f(x+a)=f(-x+a)牢记!
28.离心率爆强公式：e=sinA/(sinM+sinN)注：P为椭圆上一点，其中A为角F1PF2 ，两腰角为M ， N