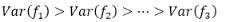
SPSS主成分分析例题详解 spss主成分分析结果解读( 二 )

文章插图
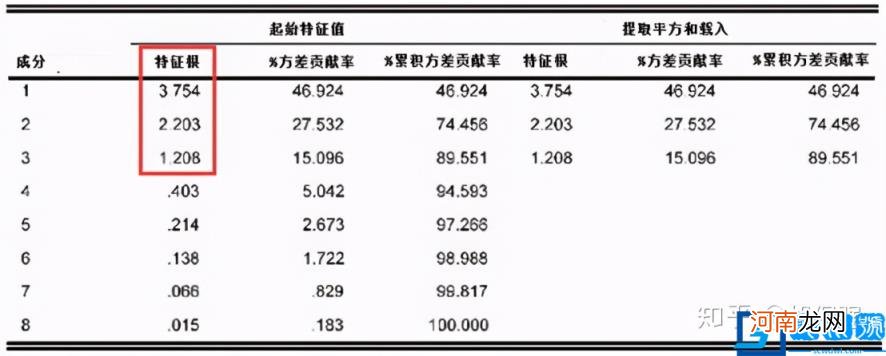
在主成分分析后，SPSS等软件会输出下面这个结果。包括特征根值，方差贡献率和累计方差贡献率。从表格结果可知，原来的变量数量是8个，经过矩阵的线性组合（正交变换）以后，形成了8个成分，前面三个成分总共贡献了数据变异的89.5%，因此提取了前面三个成分作为主成分。

文章插图
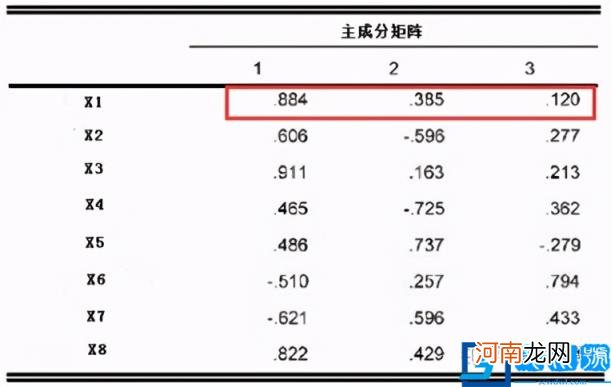
主成分分析的一个重要的结论是主成分矩阵，如下表所示。主成分矩阵可以说明各主成分在原来变量上的载荷，所以也被称为载荷矩阵。

文章插图
通过载荷矩阵可以写出主成分的组成结构表达式。我们以第一主成分为例，写出其表达式。从式子可以知道，第一主成分包含原来变量X1，X3和X8在信息最多，X2和X7其次，X4，X5和X6更少一些。这就是主成分分析的致命缺陷，提取出来的主成分不能明确解释成某几个原始变量的概率，为进一步分析制造了困难。（这个问题将由因子分析来解决）

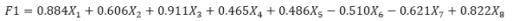
文章插图
主成分分析的另一个结论是主成分得分矩阵。其实就是主成分载荷矩阵除以主成分特征根后得到的矩阵。为什么要除以特征根呢？这是因为主成分载荷矩阵是带有成分重要性属性（包含特征根）的，如果要用提取得到的主成分进行综合排名比较或回归分析，需要先消除主成分的权重不平等（重要性不同），因此需要除以对应主成分的特征根，得到主成分得分矩阵。上表的主成分得分矩阵为：

文章插图
根据主成分得分矩阵的得分系数，就可以计算每个个案在新变量（主成分）上的数值。进而可以将新变量值用于综合评分和回归。

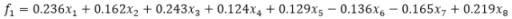
文章插图
以上就是主成分分析的所有过程。可以通过矩阵变换知道原始数据能够浓缩成几个主成分，以及每个主成分与原来变量之间线性组合关系式。但是细心的朋友会发现，每个原始变量在主成分中都占有一定的分量，这些分量（载荷）之间的大小分布没有清晰的分界线，这就造成无法明确表述哪个主成分代表哪些原始变量，也就是说提取出来的主成分无法清晰的解释其代表的含义。
因子分析
鉴于主成分分析现实含义的解释缺陷，统计学斯皮尔曼又对主成分分析进行扩展。因子分析在提取公因子时，不仅注意变量之间是否相关，而且考虑相关关系的强弱，使得提取出来的公因子不仅起到降维的作用，而且能够被很好的解释。因子分析与主成分分析是包含与扩展的关系。
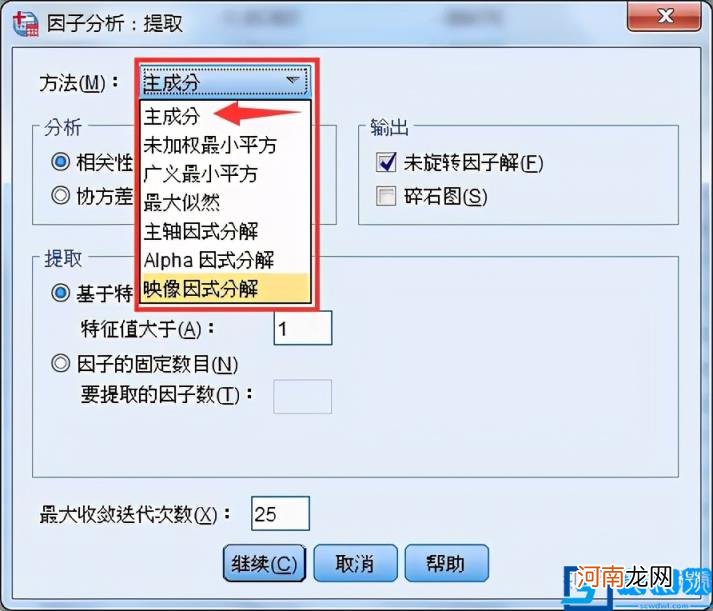
首先解释包含关系。如下图所示，在SPSS软件“因子分析”模块的提取菜单中，提取公因子的方法很多，其中一种就是主成分。由此可见，主成分只是因子分析的一种方法。

文章插图
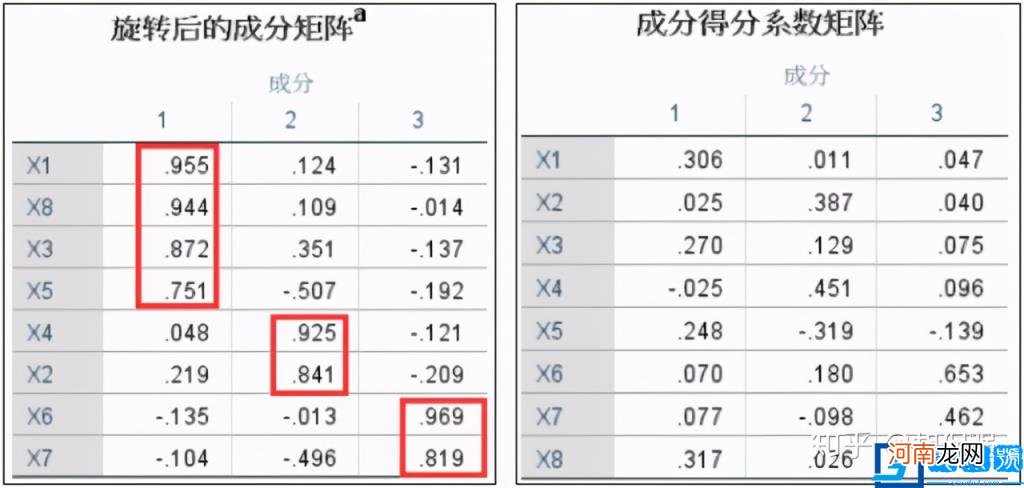
其次是扩展关系。因子分析解决主成分分析解释障碍的方法是通过因子轴旋转。因子轴旋转可以使原始变量在公因子（主成分）上的载荷重新分布，从而使原始变量在公因子上的载荷两级分化，这样公因子（主成分）就能够用哪些载荷大的原始变量来解释。以上过程就解决了主成分分析的现实含义解释障碍。