什么是分式方程什么是整式方程( 三 )

解题反思：
此题主要考查了分式方程和不等式的应用，关键是正确理解题意，找出题目中的等量关系和不等关系，列出方程和不等式。

文章插图
学好分式方程，学会用分式方程去解决问题，大家一定要认真掌握好分式的概念、分式有意义的条件、分式的乘除、乘方法则、加减运算法则、掌握分式的基本性质，并能熟练的运用基本性质进行分式的变形等。
同时要掌握好整数指数幂的概念及其性质并能熟练的运用其计算，理解分式方程的概念、解分式方程的过程，会解决可化为一元一次方程的分式方程等。
中考数学，分式方程，典型例题分析4：
“世界那么大，我想去看看”一句话红遍网络，骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场．顺风车行经营的A型车2015年6月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售价比去年增加400元，若今年6月份与去年6月份卖出的A型车数量相同，则今年6月份A型车销售总额将比去年6月份销售总额增加25%．
（1）求今年6月份A型车每辆销售价多少元（用列方程的方法解答）；
（2）该车行计划7月份新进一批A型车和B型车共50辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
A、B两种型号车的进货和销售价格如表：

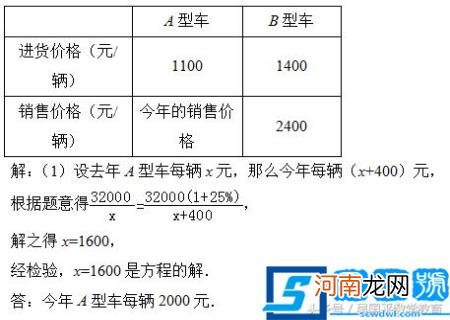
文章插图
（2）设今年7月份进A型车m辆，
则B型车（50﹣m）辆，获得的总利润为y元，
根据题意得50﹣m≤2m
【什么是分式方程什么是整式方程】解之得m≥50/3 ，
∵y=（2000﹣1100）m （2400﹣1400）（50﹣m）=﹣100m 50000 ，
∴y随m 的增大而减小，
∴当m=17时，可以获得最大利润．
答：进货方案是A型车17辆， B型车33辆．
题干分析：
（1）设去年A型车每辆x元，那么今年每辆（x 400）元，列出方程即可解决问题．
（2）设今年7月份进A型车m辆，则B型车（50﹣m）辆，获得的总利润为y元，先求出m的范围，构建一次函数，利用函数性质解决问题．
解题反思：
不同考查一次函数的应用、分式方程等知识，解题的关键是设未知数列出方程解决问题，注意分式方程必须检验，学会构建一次函数，利用一次函数性质解决实际问题中的最值问题，属于中考常考题型。
在解决一些分式方程相关问题的时候，我们需要用到换元法的数学思想方法。换元法指的是当分式方程具有某种特殊形式，一般的去分母不易解决时，可考虑用换元法。
换元法作为中学数学学习当中的一个重要的数学思想，其应用非常广泛，大家一定要认真掌握好。
解分式方程，除了要掌握好分式方程的一般解法和分式方程验根方法，大家更要进一步掌握可化为一元一次方程的分式方程的解法，熟练掌握解分式方程的技巧。从而充分理解解分式方程的基本思想是把分式方程转化成整式方程，把未知问题转化成已知问题，从而渗透数学的转化思想。