著名数学家高斯的故事简介数学家高斯简介( 二 )

文章插图

的方程的解的问题；这一部分所发展出来的技术，成了后来一代代数论学家所做的大量工作的基础。第6部分由各种不同的应用所组成。最后一部分起初吸引了最多的关注，处理的是次数为素数的割圆方程的解。
高斯把勒让德在两年前发表的二次互反律称作黄金定律。在后来的作品中，高斯试图得出同余式x^n=p(modq)对于n=3和4的类似定理；
但对这两种情况，他发现有必要把“整数”这个词的意义扩大到包括所谓的高斯整数，亦即形如a+bi的整数，式中，a和b都是整数。高斯整数构成了一个整环，像实整数整环一样，但更一般。
可整除性的问题变得更复杂，因为5不再是一个素数，可分解为两个“素数”1+2i和1-2i的乘积。
事实上，任何形如4n+1的实素数都不是“高斯素数”，而形如4n-1的实素数依然是一般化意义上的素数。
在高斯的《算术研究》中，包括了算术基本定理，它是在高斯整数的整环中继续有效的基本原理之一。事实上，任何一个因子分解是唯一的整环今天都被称作高斯整环。
《算术研究》的贡献之一是下面这个定理的证明，这个定理自欧几里得时代以来就被人所知：
任何一个正整数都可以用一种、且只能用一种方式表示为素数的乘积。
高斯关于素数的发现，并没有全都包含在《算术研究》中。在他还是一个14岁的孩子时，高斯就在一张对数表的背面，用德文写下了这样一行隐晦的文字：

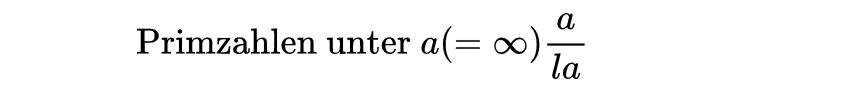
文章插图

这行文字说的是一个著名的素数定理：小于给定整数a的素数的个数在a无穷递增时趋近于a/lna 。
正如我们已经看到的那样，勒让德曾经接近于预先发现这个定理；但奇怪的是，正如我们所推测的那样，高斯写下了这个定理，但他一直对这个巧妙的结论保守秘密。
【著名数学家高斯的故事简介数学家高斯简介】 我们不知道他是否证明了这个定理，甚至也不知道他何时写下了这个定理的陈述。素数的分布对数学家有着强烈的吸引力。

著名数学家高斯的故事简介 数学家高斯简介( 二 )

著名数学家高斯的故事简介数学家高斯简介( 二 )