数学史上有趣的小故事数学历史故事( 五 )

k=1时，三维空间是球状的，总体积是有限的，其值为2R(t) 。
k=-1时，三维空间是双曲空间，总体积是无限的。
k=0时，三维空间是平直的，总体积也是无限的。
由于宇宙膨胀的速率是时间函数，会随宇宙的几何特性而有不同，所以宇宙的形状将会决定宇宙的终极命运。但值得留意的是，FRW度规是并不考虑暗能量的。
５、什么叫德西特宇宙：1917年，荷兰天文学家德西特继爱因斯坦之后提出的一个宇宙模型。它与爱因斯坦静态宇宙模型一样，认为宇宙的空间不随时间而变，故属静态型。但是，它又认为宇宙的物质有运动，不过物质的平均密度趋近于零。在这些条件下，求解爱因斯坦引力场方程，得德西特静态时空度规。
６、什么叫哥德尔宇宙：哥德尔的宇宙表明，宇宙的旋转以一种极端的方式扭曲了空间，以至于把时间都闭合了。哥德尔证明，这样的宇宙满足爱因斯坦场方程，但不满足牛顿引力。

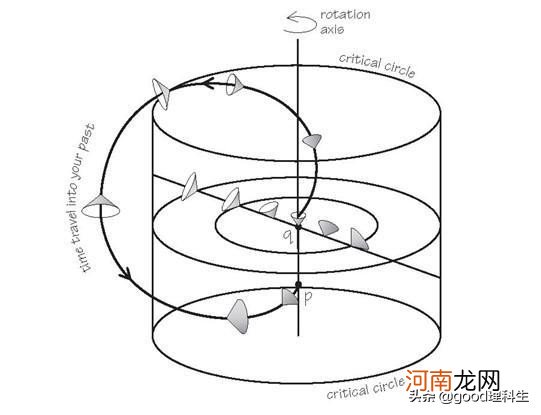
文章插图
哥德尔的宇宙是一个不断旋转的宇宙。这种宇宙不膨胀，所有的物质都绕着一个对称轴匀速转动。其中也包含了爱因斯坦的宇宙学常数，但不同的是，这里的宇宙学常数小于零，因此产生的是引力，和物质的引力一起抵消了转动产生的离心力。这本身就够有趣的了，但哥德尔的宇宙还有一个完全令人无法想象的性质：它允许时间旅行。哥德尔证明，时空中的一些路径形成了闭合的回路。大多数人，包括爱因斯坦，都相信这种事情应该违背了其他的物理定律，并且会导致科幻电影里经常演到的逻辑悖论（例如，杀死婴儿时期的自己）。
７、什么叫托布-NUT度规：托布-NUT度规是一个爱因斯坦场方程的精确解，为广义相对论的框架下所建构出的宇宙模型。
托布-NUT度规是由亚伯拉罕·哈斯克尔·托布（Abraham Haskel Taub）发现，并由以斯拉·纽曼（Ezra T. Newman）、T. 昂蒂（T. Unti）和 L. 坦布里诺（L.Tamburino）拓展到更大的流形，其首字母缩写组成了“托布-NUT”当中的“NUT” 。托布的解是爱因斯坦方程在空的空间中的一个解，表达了一种一种均匀却又各向异性的宇宙模型。
８、什么叫反反德西特空间：数学与物理学中，一个n维反德西特空间，标作AdSn为一最大对称的洛伦兹流形，具有负常数的数量曲率。其为双曲空间的洛伦兹类比，一如闵可夫斯基空间与德西特空间分别为欧几里得空间与椭圆空间的类比。
反德西特空间最知名的应用是在AdS/CFT对偶。“德西特”是以威廉·德西特（1872–1934）为名，他与阿尔伯特·爱因斯坦于1920年代一同研究宇宙中的时空结构。
以广义相对论的语言来说，反德西特空间为爱因斯坦场方程的最大对称真空解，其带有负的（吸引性）的宇宙常数，对应到负的真空能量密度与正压力。
数学中，反德西特空间有时更广义地定义为一个具有任意度规标记(p, q)的空间。物理学的情形中，一维类时维度才有意义。由于标记习惯的不同，可写作(n1, 1)或(1, n1) 。
上面所有的，包括爱氏场方程推导和目前场方程著名的解，都是为我下面的推论做铺垫，也是为大家学习提供资料。
总结一下你会发现，所有的解都是特殊的，这种特殊表现在“对称”，“真空”，“黑洞”，“趋于无限大，或无限小” 。有的是在解的基础上再解，比如史瓦西解发展为克尔解。有的解是解的反面。
这时候你会说什么？一个词叫：“乱象丛生。”正好描述这样的情况。
大的方向不对，大玩数学游戏，会使得我们越来越迷茫。去看看弦理论和无数种黑洞性质的推想，就知道这样的情况有多严重。

数学史上有趣的小故事 数学历史故事( 五 )

数学史上有趣的小故事数学历史故事( 五 )