文章插图
，所以

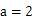
文章插图
，即；
又设

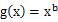
文章插图
，点在的图象上，所以

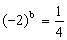
文章插图
，所以

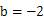
文章插图
，即

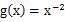
文章插图
。
在同一坐标系下画出函数和的图象，如图所示，则有

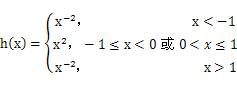
文章插图
。

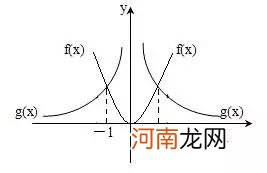
文章插图
根据图象可知函数的最大值等于

文章插图
，其单调递增区间是（

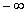
文章插图
，－1）和（0，1）；单调递减区间是

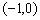
文章插图
和

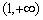
文章插图
。
例5、已知幂函数

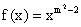
文章插图

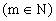
文章插图
是偶函数，且在上是减函数，求函数的解析式，并讨论

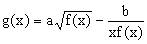
文章插图
的奇偶性 。
分析：先根据单调性求出m的取值范围，再由奇偶性进一步确定m的取值 。讨论

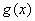
文章插图
的奇偶性时要注意对字母的讨论 。
解答：由在上是减函数得

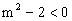
文章插图
，

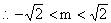
文章插图
。∵

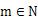
文章插图
，

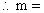
文章插图
0，1 。
又因为是偶函数，∴只有当

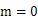
文章插图
时符合题意，故

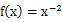
文章插图
。
于是

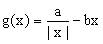
文章插图
，

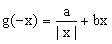
文章插图
。
当

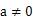
文章插图
且

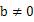
文章插图
时，为非奇非偶函数；
当

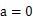
文章插图
且时，为奇函数；
当且

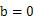
文章插图
时，为偶函数；
当且时，为既奇又偶函数 。
例6、已知幂函数

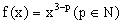
文章插图
在

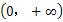
文章插图
上是增函数，且在定义域上是偶函数 。
（1）求的值，并写出相应的函数的解析式；
（2）对于（1）中求得的函数，设函数

• 妊娠便秘的缓解措施 孕期妈妈便秘怎么办
• 适宜孕妇饮用的茶类 怀孕期间的孕妇可以喝茶吗
• 孕妇喝什么饮品比较好 碳酸饮料对孕妇的6大伤害
• 女人怀孕时能吃的五谷杂粮 孕妇可以吃绿豆吗
• 孕妈吃火锅的注意事项 孕妈究竟能不能吃火锅
• 怀孕妇女专门挑选的水果 孕妇女吃什么水果好
• 准妈妈如何科学吃虾呢 怀孕与小龙虾的那些事儿
• 16万元的特斯拉要来了 明年或在中国推出
• 热度远低于双11，今年双12要凉？
• 狗猫鼠故事情节概括及主旨 狗猫鼠的主要内容简单概括