勾股定理16种证明方法( 二 )

F作FN⊥PQ，垂足为N. ∵ ∠BCA = 90o，QP∥BC，∴ ∠MPC = 90o，∵ BM⊥PQ，∴ ∠BMP = 90o，∴ BCPM是一个矩形，即∠MBC = 90o. ∵ ∠QBM + ∠MBA = ∠QBA = 90o，
∠ABC + ∠MBA = ∠MBC = 90o，∴ ∠QBM = ∠ABC，
又∵ ∠BMP = 90o，∠BCA = 90o，BQ = BA = c，
∴ RtΔBMQ ≌ RtΔBCA.
同理可证RtΔQNF ≌ RtΔAEF.
从而将问题转化为【证法4】（梅文鼎证明）.

文章插图
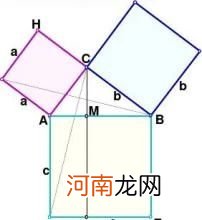
【证法7】（欧几里得证明）
做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结 BF、CD. 过C作CL⊥DE，
交AB于点M，交DE于点
L. K∵ AF = AC，AB = AD，∠FAB = ∠GAD，∴ ΔFAB ≌ ΔGAD，12a∵ ΔFAB的面积等于2，
ΔGAD的面积等于矩形ADLM
的面积的一半，
∴ 矩形ADLM的面积 =a
同理可证，矩形MLEB的面积 =b.
∵ 正方形ADEB的面积 = 矩形ADLM的面积 + 矩形MLEB的面积
∴ c=a+b。

文章插图
【证法8】（利用相似三角形性质证明）
如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.
在ΔADC和ΔACB中，∵ ∠ADC = ∠ACB = 90o，
∠CAD = ∠BAC，∴ ΔADC ∽ ΔACB.
AD∶AC = AC ∶AB，
即 AC=ADXAB.
同理可证，ΔCDB ∽ ΔACB，从而有 BC=BDxAB.
∴ AC+BC=(AD+DB)xAB=AB，即 a+b=c、
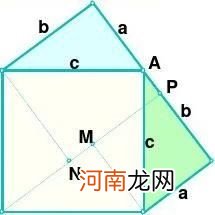
【证法9】（杨作玫证明）
做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形. 过A作AF⊥AC，AF交GT于F，AF交DT于R. 过B作BP⊥AF，垂足为P. 过D作DE与CB的延长线垂直，垂足为E，DE交AF于H. ∵ ∠BAD = 90o，∠PAC = 90o，
∴ ∠DAH = ∠BAC. 又∵ ∠DHA = 90o，∠BCA = 90o，AD = AB = c，∴ RtΔDHA ≌ RtΔBCA.
∴ DH = BC = a，AH = AC = b
由作法可知，PBCA 是一个矩形，
所以 RtΔAPB ≌ RtΔBCA. 即PB =
CA = b，AP= a，从而PH = b―a.
∵ RtΔDGT ≌ RtΔBCA ,
RtΔDHA ≌ RtΔBCA.
∴ RtΔDGT ≌ RtΔDHA .
∴ DH = DG = a，∠GDT = ∠HDA .
又∵ ∠DGT = 90o，∠DHF = 90o，
∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90o，
∴ DGFH是一个边长为a的正方形.
∴ GF = FH = a . TF⊥AF，TF = GT―GF = b―a .
∴ TFPB是一个直角梯形，上底TF=b―a，下底BP= b，高FP=a +（b―a）. 用数字表示面积的编号（如图），则以c为边长的正方形的面积为
c=S+S+S+S+S ①
∵ S+S+S=1/2[b+(b-a)]x[a+(b-a)]=b-1/2ab
S=S+S
∴S+S=b-1/2ab-S=b-S-S ②
把②代入①，得
C=S+S+b-S-S+S+S
=b+S+S=b+a
∴ a+b=c.

文章插图
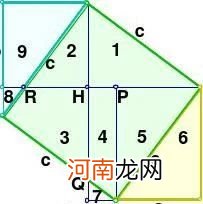
【证法10】（李锐证明）
设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c. 做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使A、E、G三点在一条直线上. 用数字表示面积的编号（如图）.
∵ ∠TBE = ∠ABH = 90o，∴ ∠TBH = ∠ABE. R又∵ ∠BTH = ∠BEA = 90o，
BT = BE = b，∴ RtΔHBT ≌ RtΔABE. ∴ HT = AE = a. ∴ GH = GT―HT = b―a. 又∵ ∠GHF + ∠BHT = 90o，∠DBC + ∠BHT = ∠TBH + ∠
∴ ∠GHF = ∠DBC. ∵ DB = EB―ED = b―a，
∠HGF = ∠BDC = 90o，
∴ RtΔHGF ≌ RtΔBDC. 即 S=S.
过Q作QM⊥AG，垂足是M. 由∠BAQ = ∠BEA = 90o，可知 ∠ABE
= ∠QAM，而AB = AQ = c，所以RtΔABE ≌ RtΔQAM . 又RtΔHBT ≌ RtΔABE. 所以RtΔHBT ≌ RtΔQAM . 即 S=S.
由RtΔABE ≌ RtΔQAM，又得QM = AE = a，∠AQM = ∠BAE.