勾股定理16种证明方法

勾股定理是一个基本的平面几何定理，也是数学中最重要的定理之一。在初中的数学课程中，大家都是学过的。其实勾股定理有很多种方式证明哦，下面小编就整理了勾股定理16种经典证明方法，经典不容错过哦！
【证法1】（课本的证明）
做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.
从图上可以看到，这两个正方形的边长都是a + b，所以面积相等. 即a+b+4x1/2ab=c+4x1/2ab，整理得a+b=c 。

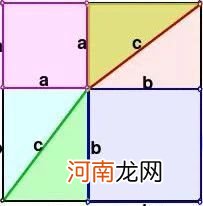
文章插图

【证法2】（邹元治证明）
以a、b 为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角1ab2形的面积等于. 把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上. ∵ RtΔHAE ≌ RtΔEBF, ∴ ∠AHE = ∠BEF.
∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o.
∴ 四边形EFGH是一个边长为c的
正方形. 它的面积等于c2. ∵ RtΔGDH ≌ RtΔHAE,
∴ ∠HGD = ∠EHA. ∵ ∠HGD + ∠GHD = 90o,
∴ ∠EHA + ∠GHD = 90o.
又∵ ∠GHE = 90o,
∴ ∠DHA = 90o+ 90o= 180o.
∴ ABCD是一个边长为a + b的正方形，它的面积等于(a+b).
∴(a+b)=4x1/2ab+c
∴ a+b=c 。
【证法3】（赵爽证明）
以a、b 为直角边（b>a），以c为斜边作四个全等的直角三角形，则每个直角 1ab2三角形的面积等于. 把这四个直角三
角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,
∴ ∠HDA = ∠EAB.
∵ ∠HAD + ∠HAD = 90o，
∴ ∠EAB + ∠HAD = 90o，2∴ ABCD是一个边长为c的正方形，它的面积等于c.
∵ EF = FG =GH =HE = b―a ,
∠HEF = 90o.
∴ EFGH是一个边长为b―a的正方形，它的面积等于(b-a).
∴(b-a)=4x1/2ab+c
∴ a+b=c 。
【证法4】（1876年美国总统Garfield证明）
以a、b 为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角1ab形的面积等于2. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上. ∵ RtΔEAD ≌ RtΔCBE,
∴ ∠ADE = ∠BEC. ∵ ∠AED + ∠ADE = 90o, ∴ ∠AED + ∠BEC = 90o.
∴ ∠DEC = 180o―90o= 90o. ∴ ΔDEC是一个等腰直角三角形，12c2它的面积等于.
又∵ ∠DAE = 90o, ∠EBC = 90o,
∴ AD∥BC.
∴ ABCD是一个直角梯形，它的面积等于1/2(a+b).
∴1/2(a+b)=2x1/2ab+1/2c
∴ a+b=c 。

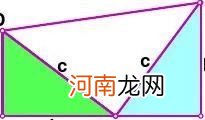
文章插图
【证法5】（梅文鼎证明）
做四个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c. 把它们拼成如图那样的一个多边形，使D、E、F在一条直线上. 过C作AC的延长线交DF于点P.
∵ D、E、F在一条直线上, 且RtΔGEF ≌ RtΔEBD,
∴ ∠EGF = ∠BED，
∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，
∴ ∠BEG =180o―90o= 90o. 又∵ AB = BE = EG = GA = c，
∴ ABEG是一个边长为c的正方形. ∴ ∠ABC + ∠CBE = 90o.
∵ RtΔABC ≌ RtΔEBD,
∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90o. 即 ∠CBD= 90o. 又∵ ∠BDE = 90o，∠BCP = 90o，BC = BD = a.
∴ BDPC是一个边长为a的正方形.
同理，HPFG是一个边长为b的正方形.
设多边形GHCBE的面积为S，则
a+b=S+2x1/2ab,
c=S+2x1/2ab
∴a+b=c.
证法6】（项明达证明）
做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形，使E、A、C三点在一条直线上. 过点Q作QP∥BC，交AC于点P. 过点B作BM⊥PQ，垂足为M；再过点