三角形和半圆形的组合

这是初中几何基础题，据说是基础题，但有点提高，对测试基础知识的灵活运用有一定的要求。这个问题所需的阴影部分真的很小，很多学生不知道从哪里开始。
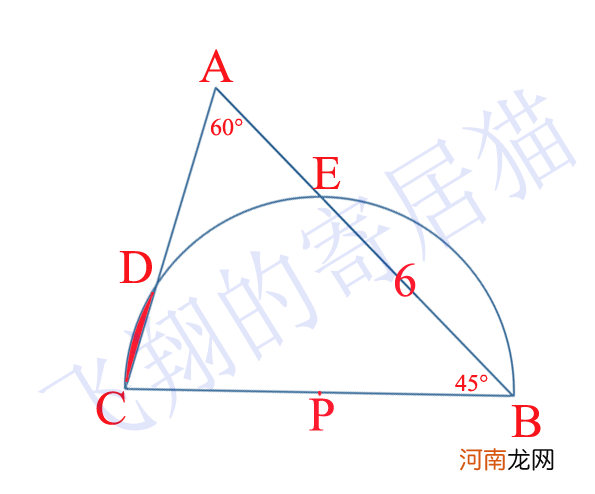
主题：三角形ABC，∠A=60°，∠B=45°，以BC直径为半圆，P半圆交三角形交三角形ABC于D、E两点，已知BE长度为6，左边一小块的红色阴影面积是多少？

文章插图

【三角形和半圆形的组合】首先，当你看到半圆直径的条件时，你应该能够认为直径对应的角度是直角，因此连接CE，∠CEB就是90°，而∠B又是45度，所以三角形CEB就是等腰直角三角形，顺便勾股定理就能找到圆直径。
在三角形CAE中，∠A=60°，则∠ACE=90-60=30°，意味着DE弧对应的圆周角为30度，然后连接PD,PE，则DE弧对应的圆心角是圆周角的两倍，即∠DPE=60°，那么DC这个弧，也就是标题要求的阴影部分对应的弧，对应的圆心角是∠DPC=90°-60°=30°
求出了这个圆心角，那么剩下的就好做了，阴影部分的面积就是扇形PCD - 三角形PCD，其中三角形PCD的高是30°角对应的是半径的一半。
所以题目不是很难，但是需要灵活运用基础知识才能得到最终答案。