比例系数k 比例系数的几何意义和七个常考模型K的几何意义

一.反比例函数的概念

概念：一般，函数y=k/x（k是常数， k≠0）称为反比例函数。反比例函数的分析也可以写成形式。x值的范围是x≠0所有实数，函数的值范围也是所有非零实数。

文章插图
注：(1)比例系数k≠0它是定义反比例函数的重要组成部分；
(2)反比例函数的分析， k,x,y均不等于0;
(3)反比例函数中的两个变量必须成反比例关系，
反之,则不一定成立
例1 给出的六种关系类型：①x(y 1); ②y=2/(x 2); ③y=1/x2; ④y=1/2x; ⑤y=x/2 ; ⑥y=-3/x.其中y是x(
【比例系数k 比例系数的几何意义和七个常考模型K的几何意义】A.①②③④⑥B.③⑤⑥C.①②④D.④⑥
例2 若函数
是y关于x反比例函数，则m=.
3 正比例函数y=-x/3和反比例函数y=-1/3x？
A.自变量x的指数相同B.相同的比例系数
C.自变量x相同的， D.函数y取值范围相同

文章插图
2.易错点分析漏掉k≠0这一条件
在回答与反比例函数相关的问题时，应注意系数k≠0它是反比例函数定义的重要组成部分，不能错过这种条件.
例4已知函数
对于反比例函数，则k=.
二.图像和性质的反比例函数
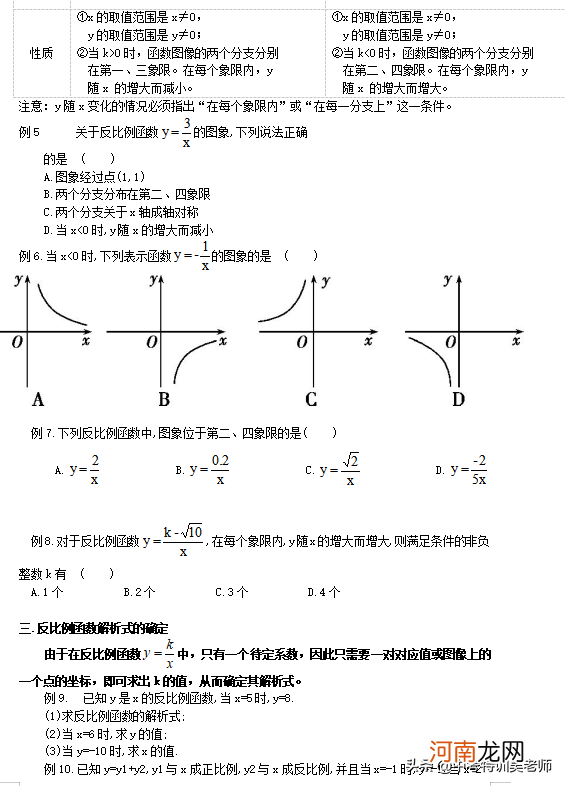
1.反比函数的图像是双曲线，它有两个分支，分别位于第一、三象限或第二、四象限，它们是对称的原点。因为反比函数中的自变量x≠0 ，函数y≠0 ，因此，它的图像和x轴、y轴没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。
2.反比例函数的性质

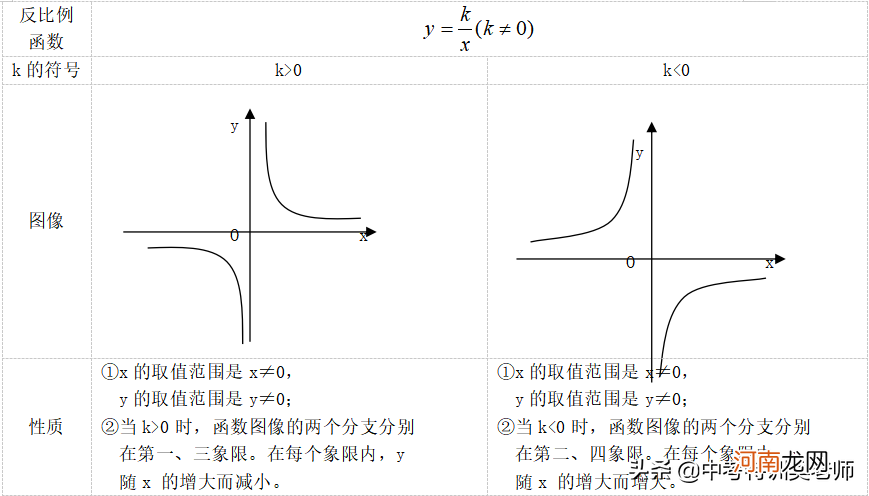
文章插图
注意：y随x变化必须指出在每个象限内或在每个分支上的条件。
5 反比例函数y=3/x图
A.图像经过点(1 ， 1)
B.两个分支分布在第二和第四象限
C.关于两个分支x轴成轴对称
D.当x<0时,y随x增加和减少
例6.当x<0以下表示函数y=-1/x()

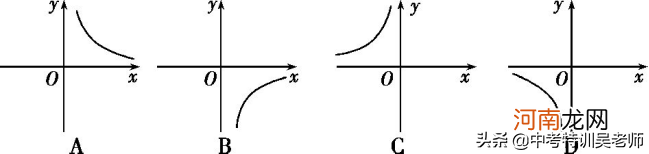
文章插图
例7.图像位于第二，
A.y=2/x?B.y=0.2/x?C.y=√2/x?D.y=-2/5x?
例8.反比例函数y=(k-√10)/x,在每个象限内， y随x增加和增加，满足条件的非负整数k(
A.1个B.2个C.3个D.4个

文章插图
三.确定反比例函数解析式
由于反比例函数中只有一个待定系数，因此只需在图像上找到一对相应值或一个点的坐标即可k从而确定其分析类型。
例9.　已知y是x当x=5时,y=8.
(1)求反比例函数的分析；
(2)当x=6时,求y的值;
(3)当y=-10时,求x的值.
例10.已知y=y1 y2,y1与x成正比例,y2与x成反比例，当x=-1时,y=-1,当x=2
时,y=5.
(1)求y关于x函数关系；
(2)当y=-5时,求x的值.
四.反比例系数k几何意义及其常见模型
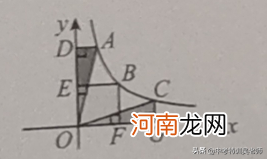
1.(图片中常见的模型结论和证明过程)如下图所示，任何反比函数图像P作x轴、y轴的垂线PM ， PN ，获得的矩形BEOF的面积S=BEBF= 。

文章插图

文章插图
注：(1)使用k几何意义求k一定要注意计算的问题k的绝对值；
(2)反比例函数图像在第三象限时， k为正。
2.三角形梯形模型
3.比例线段模型
4.等线段模型
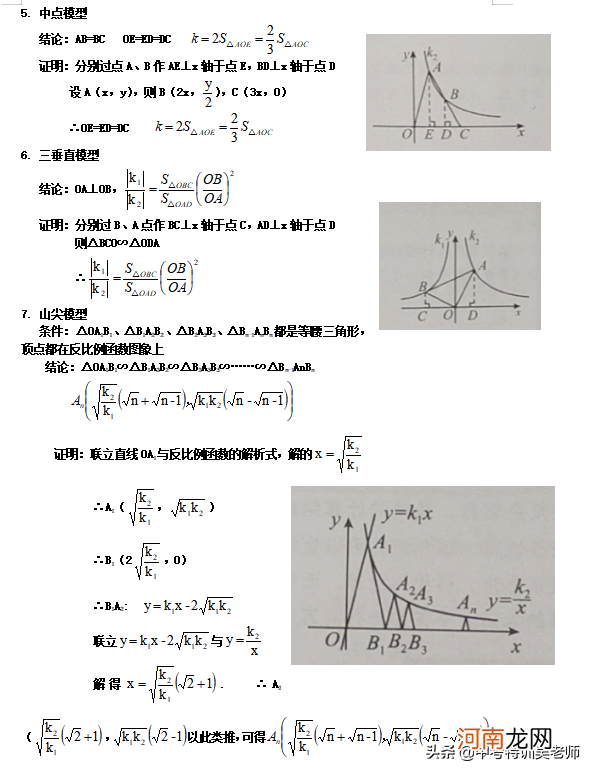
5.中点模型
6.三垂直模型
7.山尖模型
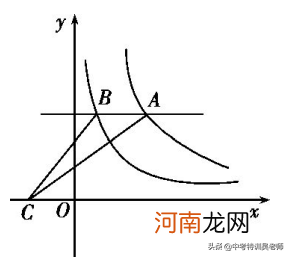
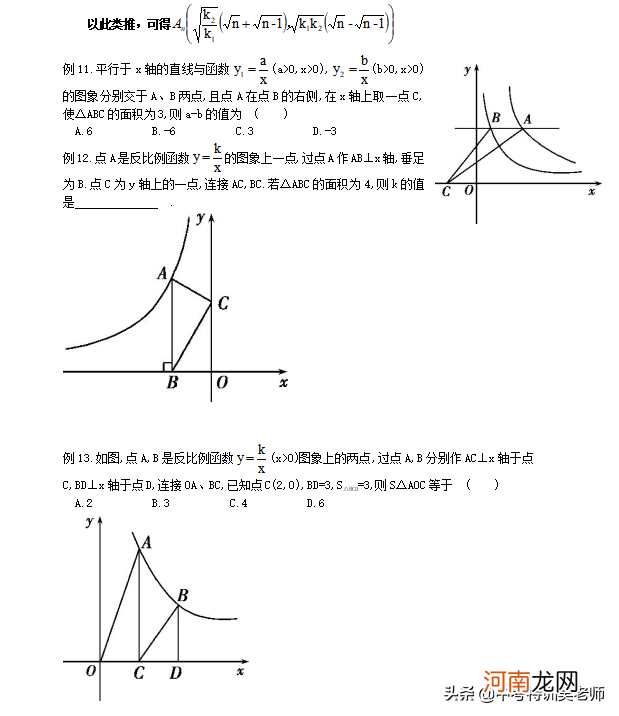
例11.平行于x轴的直线和函数y1=a/x(a>0,x>0),y2=b/x(b>0,x>0)图像分别交A、B两点,且点A在点B的右侧,在x轴上取一点C,使△ABC面积为3 ，则a-b()
A.6B.-6C.3D.-3

文章插图
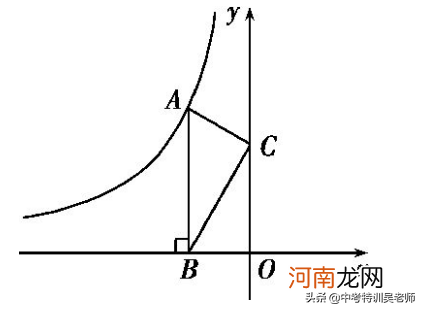
例12.点A是反比函数y=k/x一点图像，过点A作AB⊥x轴,垂足为B.点C为y轴上的一点，连接AC,BC.若△ABC4 ，然后k」.

文章插图
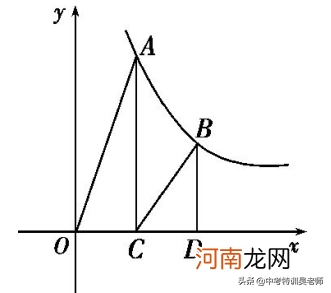
例13.如图,点A,B是反比函数y=k/x(x>0)图像上的两点，过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCD=3,则S△AOC(
A.2B.3C.4D.6

文章插图